Claudia Tevez
Algoritmos de ordenamiento
El ordenamiento es una labor común que realizamos continuamente. ¿Pero te has preguntado qué es ordenar? ¿No? Es que es algo tan corriente en nuestras vidas que no nos detenemos a pensar en ello. Ordenar es simplemente colocar información de una manera especial basándonos en un criterio de ordenamiento.
En la computación el ordenamiento de datos también cumple un rol muy importante, ya sea como un fin en sí o como parte de otros procedimientos más complejos. Se han desarrollado muchas técnicas en este ámbito, cada una con características específicas, y con ventajas y desventajas sobre las demás. Aquí voy a mostrarte algunas de las más comunes, tratando de hacerlo de una manera sencilla y comprensible.
La siguiente es una tabla comparativa de algunos algoritmos de ordenamiento:

Ordenamiento burbuja:
Este es el algoritmo más sencillo probablemente. Ideal para empezar. Consiste en ciclar repetidamente a través de la lista, comparando elementos adyacentes de dos en dos. Si un elemento es mayor que el que está en la siguiente posición se intercambian.
Ejemplo:
Como se muestra en la siguiente figura, en la primera iteración se lleva el máximo a su posición definitiva al final del arreglo.
En la segunda iteración se lleva el segundo máximo a su posición definitiva. Y así continúa hasta ordenar todo el arreglo. Observe que si en un recorrido secuencial no se intercambia ningún elemento, el arreglo está ordenado y se puede concluir.
Ordenamiento por selección
Aplicacion en c++


El ordenamiento por selección (Selection Sort en inglés) es un algoritmo de ordenamiento que requiere operaciones para ordenar una lista de n elementos.
Su funcionamiento es el siguiente:
-
Buscar el mínimo elemento de la lista
-
Intercambiarlo con el primero
-
Buscar el mínimo en el resto de la lista
-
Intercambiarlo con el segundo
Y en general:
-
Buscar el mínimo elemento entre una posición i y el final de la lista
-
Intercambiar el mínimo con el elemento de la posición i
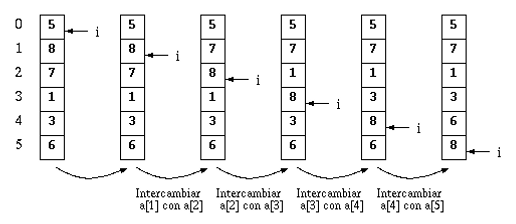
El algoritmo de selección y reemplazo ordena los elementos de un arreglo nativo sin utilizar un segundo arreglo. El algoritmo se basa en la siguiente idea. En el arreglo ordenado, el mínimo debe quedar en a[0], de modo que se ubica su posición real en el arreglo. Por ejemplo, se determina que está en a[3] como lo indica el primer arreglo de izquierda a derecha en la siguiente figura:

Entonces se procede a intercambiar los valores de a[0] con a[3]. Ahora, a[0] contiene el valor correcto y por lo tanto, nos olvidamos de él. A continuación, el algoritmo ordena el arreglo desde el índice 1 hasta el 5, ignorando a[0]. Por lo tanto, ubica nuevamente la posición del mínimo entre a[1], a[2], ..., a[5] y lo intercambia con el elemento que se encuentra en a[1] como se indica en el segundo arreglo de la figura. Ahora, a[0] y a[1] contienen los valores correctos. Y así el algoritmo continúa hasta que a[0], a[1], ..., a[5] tengan los valores ordenados.
Ordenamiento por inserción
Aplicacion en c++
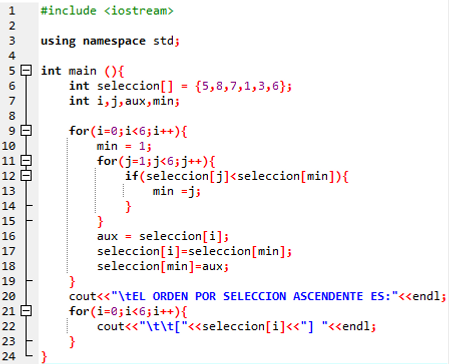

El ordenamiento por inserción es una manera muy natural de ordenar para un ser humano, y puede usarse fácilmente para ordenar un mazo de cartas numeradas en forma arbitraria.
La idea de este algoritmo de ordenación consiste en ir insertando un elemento de la lista ó un arreglo en la parte ordenada de la misma, asumiendo que el primer elemento es la parte ordenada, el algoritmo ira comparando un elemento de la parte desordenada de la lista con los elementos de la parte ordenada, insertando el elemento en la posición correcta dentro de la parte ordenada, y así sucesivamente hasta obtener la lista ordenada.

Aplicacion en c++


Ordenamiento Shell
El método se denomina así en honor de su inventor Donald Shell.
El algoritmo Shell es una mejora de la ordenación por inserción, donde se van comparando elementos distantes, al tiempo que se los intercambian si corresponde. A medida que se aumentan los pasos, el tamaño de los saltos disminuye; por esto mismo, es útil tanto como si los datos desordenados se encuentran cercanos, o lejanos.
Es bastante adecuado para ordenar listas de tamaño moderado, debido a que su velocidad es aceptable y su codificación es bastante sencilla. Su velocidad depende de la secuencia de valores con los cuales trabaja, ordenándolos.El siguiente ejemplo muestra el proceso de forma gráfica:
Considerando un valor pequeño que está inicialmente almacenado en el final del vector. Usando un ordenamiento O(n2) como el ordenamiento de burbuja o el ordenamiento por inserción, tomará aproximadamente n comparaciones e intercambios para mover este valor hacia el otro extremo del vector.
El Shell sort primero mueve los valores usando tamaños de espacio gigantes, de manera que un valor pequeño se moverá bastantes posiciones hacia su posición final, con sólo unas pocas comparaciones e intercambios.
Ejemplo:
Considere una lista de números como [13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10]. Si comenzamos con un tamaño de paso de 8, podríamos visualizar esto dividiendo la lista de números en una tabla con 5 columnas. Esto quedaría así:

Entonces ordenamos cada columna, lo que nos queda:

Cuando lo leemos de nuevo como una única lista de números, obtenemos [ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ]. Aquí, el 10 que estaba en el extremo final, se ha movido hasta el extremo inicial.
Esta lista es entonces de nuevo ordenada usando un ordenamiento con un espacio de 3 posiciones, y después un ordenamiento con un espacio de 1 posición (ordenamiento por inserción simple).

Aplicacion en c++

Ordenamiento Quicksort
El algoritmo Quicksort o también llamado algoritmo de ordenamiento Rapido, es un algoritmo de ordenamiento de datos, que usa recursividad para poder ordenarlo, ademas que hace comparaciones entre un pivote seleccionado y sus demás elementos del arreglo, y va recorriendo dos contadores que indican la posicion de dos elementos uno inicial y un final, y de acuerdo a las comparaciones hace un intercambio entre los valores de estos contadores.
El algoritmo fundamental es el siguiente:
-
Elegir un elemento de la lista de elementos a ordenar, al que llamaremos pivote.
-
Resituar los demás elementos de la lista a cada lado del pivote, de manera que a un lado queden todos los menores que él, y al otro los mayores. En este momento, el pivote ocupa exactamente el lugar que le corresponderá en la lista ordenada.
-
La lista queda separada en dos sublistas, una formada por los elementos a la izquierda del pivote, y otra por los elementos a su derecha.
-
Repetir este proceso de forma recursiva para cada sublista mientras éstas contengan más de un elemento. Una vez terminado este proceso todos los elementos estarán ordenados. Como se puede suponer, la eficiencia del algoritmo depende de la posición en la que termine el pivote elegido.
-
En el mejor caso, el pivote termina en el centro de la lista, dividiéndola en dos sublistas de igual tamaño. En este caso, el orden de complejidad del algoritmo es O(n·log n).
-
En el peor caso, el pivote termina en un extremo de la lista. El orden de complejidad del algoritmo es entonces de 0(n²). El peor caso dependerá de la implementación del algoritmo, aunque habitualmente ocurre en listas que se encuentran ordenadas, o casi ordenadas.
-
En el caso promedio, el orden es O(n·log n).

Aplicacion en c++


